Materi, Soal dan Pembahasan Super Lengkap Limit Tak Hingga (Soal UTBK SBMPTN, SIMAK UI,UM UGM dan UNDIP)
Pengertian Asimtot
Asimtot adalah suatu garis lurus yang didekati oleh yang didekati oleh suatu kurva baik secara tegak (asimtot tegak) atau secara mendatar (asimtot datar) atau mendekati miring (asimtot miring). Garis yang kita namakan asimtot akan senantiasa didekati oleh kurva tetapi tidak pernah bersinggungan atau tidak akan pernah berpotongan antara garis dan kurva tersebut di titik jauh tak terhingga (Jaraknya kian usang mendekati nol).
A. Asimtot Datar
Jika jarak suatu kurva kepada suatu garis datar mendekati nol,maka garis tersebut yakni asimtot datar dari kurva.
Garis y = L disebut asimtot mendatar dari grafik fungsi y = f(x) kalau memenuhi:
dengan :
B. Asimtot Tegak
Jika jarak suatu kurva kepada suatu garis vertikal mendekati nol maka garis tegak tersebut yakni asimtot tegak dari kurva.
Garis x = a disebut asimtot tegak dari fungsi y = f(x) kalau menyanggupi :
dengan:
Untuk fungsi rasional yang berbentuk
}{g(x)}) ,
,
garis x = a yakni asimtot tegak dari grafik fungsi tersebut kalau :
Untuk mengerti bahan asimtot ini, dan penggunaan rancangan di atas mari kita diskusikan pola soal berikut :
Contoh 1:
Tentukan asimtot datar dan tegak dari fungsi =\frac{x+3}{x+2})
Pembahasan:
a. Asimtot Mendatar
Untuk menyeleksi asimtot mendatar perlu dimengerti rancangan :
- Untuk nilai x mendekati
 , maka :
, maka :
- Untuk nilai x mendekati
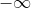 , maka :
, maka :
Sehingga asimtot mendatar =\frac{x+3}{x+2}) adalah y = 1
adalah y = 1
b. Asimtot Tegak
Untuk menyeleksi asimtot tegak perlu dimengerti rancangan :
Garis x = a disebut asimtot tegak dari fungsi y = f(x) kalau menyanggupi :
Contoh 3:
Tentukan asimtot datar dan tegak dari fungsi =\frac{x^{3}+1}{x-1})
Pembahasan:
a. Asimtot Mendatar
Untuk menyeleksi asimtot mendatar perlu dimengerti rancangan :
- Untuk nilai x mendekati
 , maka :
, maka :
Fungsi
=\frac{x^{3}+1}{x-1})
tak punya asimtot datar alasannya hasil limit adalah

untuk x 
b. Asimtot Tegak
Untuk menyeleksi asimtot tegak perlu dimengerti rancangan :
Garis x = a disebut asimtot tegak dari fungsi y = f(x) kalau menyanggupi :
Karena penyebut yakni x -1, maka karnya x = 1 sehingga persamaan asimtot tegaknya yakni x = 1 alasannya :
Contoh 4:Diketahui dari fungsi =\frac{ax+5}{\sqrt{x^{2}+bx+1}}) , dengan a > 0 dan b < 0. Jika grafik fungsi mempunyai satu asimtot tegak dan salah satunya asimtot datarnya adalah y = -3, maka a + 2b = ..............
, dengan a > 0 dan b < 0. Jika grafik fungsi mempunyai satu asimtot tegak dan salah satunya asimtot datarnya adalah y = -3, maka a + 2b = ..............
Pembahasan:
- Karena dimengerti bahwa fungsi
=\frac{ax+5}{\sqrt{x^{2}+bx+1}}) memiliki satu asimtot tegak, memiliki arti penyebutnya cuma mempunyai satu faktor. Sehingga b haruslah nilai -2 agar
memiliki satu asimtot tegak, memiliki arti penyebutnya cuma mempunyai satu faktor. Sehingga b haruslah nilai -2 agar 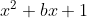 memiliki satu faktor.
memiliki satu faktor.
- Karena dimengerti asimtot mendataranya y = -3 artinya hasil limitnya yakni -3
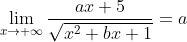
dan
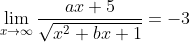
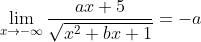
dan
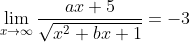
maka a = 3
Karena pada soal dibilang nila a > 0, maka nila a yang digunakan yakni a = 3.
jadi, nilai a + 2b = 3 + 2(-2) =-1
Contoh 5:
Diantara opsi berikut, kurva
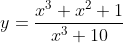
memotong asimtot datarnya di titik x =....
A. 1 B. 2 C. 3 D. 4 E. 5
Pembahasan:
Untuk menyeleksi asimtot mendatar 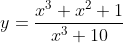
adalah dengan:
maka:
Dengan mensubsitusi nilai y = 1 ke 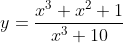 , maka diperoleh:
, maka diperoleh:
Jadi, titik potongnya yakni x = 3 tau x = -3 dan opsi jawabannya yakni x = 3 (C)
Buat lebih berguna, kongsi:
, maka diperoleh:
