Salam para Bintang
Selanjutnya kita mempelajari dan membahas bahan dan soal-soal tentang teorema sisa,teorema aspek dan duduk permasalahan habis dibagi. Soal-soal ini sungguh sering timbul di cobaan masuk Perguruan Tinggi Negeri dan cobaan Sekolah tentunya. Jadi,kalian mesti sungguh paham tentang bahan ini. Nah, eksklusif kita diskusikan secara terang di postingan ini!
A. Teorema Sisa
Dalam teorema sisa, ada beberapa hal yang perlu dimengerti yakni duduk permasalahan pembaginya. Misalanya;
- Jika f(x) dibagi (x-k) maka sisanya yakni f(k)
- Jika f(x) dibagi (x+k) maka sisanya adalah f(-k)
- Jika f(x) dibagi (ax-b) maka sisanya yakni f(b/a)
- Jika f(x) dibagi (ax+b) maka sisanya adalah f(-b/a)
- Jika f(x) habis dibagi (x-a) maka sisanya yakni f(a) = 0
Contoh 1:
Penyelesaian:
Untuk menyeleksi sisa pembagian =x^{3}-2x^{2}-3x+5) oleh
oleh 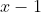 , maka kita mesti tetapkan dahulu pembuat nol dari pembagi yaitu x -1 = 0, maka x = 1
, maka kita mesti tetapkan dahulu pembuat nol dari pembagi yaitu x -1 = 0, maka x = 1
Sehingga , sisa pembagian adalah P(1) maka:
Sehingga , sisa pembagian adalah P(-2) maka:
Untuk menyeleksi sisa pembagian =2x^{2}-3x+10) oleh
oleh 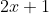 , maka kita mesti tetapkan dahulu pembuat nol dari pembagi yaitu 2x +1 = 0, maka x = -1/2
, maka kita mesti tetapkan dahulu pembuat nol dari pembagi yaitu 2x +1 = 0, maka x = -1/2
Sehingga , sisa pembagian adalah P(-1/2) maka:
Untuk menyeleksi nilai m pada pembagian =mx^{3}-2x^{2}+3x+1) oleh
oleh 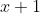 , maka kita mesti tetapkan dahulu pembuat nol dari pembagi yaitu x +1 = 0, maka x = -1, dimana habis dibagi yakni sisa = 0
, maka kita mesti tetapkan dahulu pembuat nol dari pembagi yaitu x +1 = 0, maka x = -1, dimana habis dibagi yakni sisa = 0
Sehingga , sisa pembagian adalah P(-1) = 0 maka:
Misalkan, suku banyak f(x) dibagai suku banyak g(x), diperoleh hasil baginya h(x) dan sisanya yakni s(x), maka sanggup dituliskan selaku berikut:
f(x) = g(x).h(x) + s(x)
Jika s(x) = 0, maka f(x) = g(x).h(x), artinya g(x) membagi f(x) atau dengan kata lain g(x) maupun h(x) ialah aspek dari f(x)
Kesimpulan,
- Jika (x-k) yakni aspek dari P(x) , maka P(k) = 0
- Jika (x +k) yakni aspek dari P(x) , maka P(-k) = 0
- Jika (ax+k) yakni aspek dari P(x), maka P( -k/a) = 0
- Jika (ax-k) yakni aspek dari P(x), maka P(k/a) = 0
Untuk menyeleksi nilai m, karena 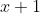 adalah aspek dari suku banyak
adalah aspek dari suku banyak =mx^{3}-2x^{2}+3x+1) , maka kita mesti tetapkan dahulu pembuat nol dari aspek yaitu x +1 = 0, maka x = -1,
, maka kita mesti tetapkan dahulu pembuat nol dari aspek yaitu x +1 = 0, maka x = -1,
Buat lebih berguna, kongsi:

