Salam Para Bintang
Kali ini kita akan membahas bahan ihwal bahan dasar untuk merencanakan diri di cobaan UTBK, Ujian Sekolah, Ujian Masuk Perguruan Tinggi Negeri lainnya. Materi ini merupakan sungguh timbul dalam aneka macam soal-soal cobaan yang diadakan apalgi mau masuk PTN. Jadi, sebelum kalian menyelesaikan soal-soal kedudukan dua bulat fungsi, maka pasti saja ketahui dahulu materinya ya. Oke !
A. Kedudukan Dua Lingkaran
Kedudukan dua bulat meninjukkan bagaimana posisi dari bulat pertama dengan bulat kedua. Hubungan (kedudukan) dua bulat terdiri atas empat kemungkinan yaitu:
1. Tidak Berpotongan, tapi di luar sesamanya
Perhatikan gambar berikut!

Dari gambar di atas, berbincang bahwa lingkaran 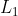 dengan jari-jari
dengan jari-jari 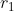 dan lingkaran
dan lingkaran 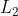 dengan jari-jari
dengan jari-jari  , dimana
, dimana 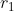 >
>  . Misalkan d = jarak sentra lingkaran
. Misalkan d = jarak sentra lingkaran 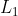 dan
dan 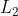 .
.

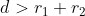
Jadi, jika 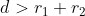 maka lingkaran
maka lingkaran 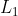 dan
dan 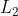 tidak berpotongan, tapi di luar sesamanya.
tidak berpotongan, tapi di luar sesamanya.
2. Bersinggungan di luar
Perhatikan gambar berikut!
Dari gambar di atas diperoleh, jika  =
= 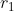 +
+  , maka lingkaran
, maka lingkaran 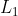 dan lingkaran
dan lingkaran 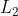 saling bersentuhan .
saling bersentuhan .
3. Lingkaran yang satu di dalam bulat lainnya. Kedudukan Lingkaran yang satu di dalam bulat yang lain terdiri atas 3 jenis yaitu:
- Lingkaran pertama bersentuhan dengan bulat 2 di dalam
- Lingkaran pertama dengan bulat 2 sepusat
- Lingkaran pertama tidak bersinggungan dan tidak sepusat dengan bulat 2
 |
| Lingkaran pertama bersentuhan dengan bulat 2 di dalam |
Dari gambar di atas diperoleh lingkaran 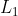 dengan jari-jari
dengan jari-jari 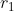 dan lingkaran
dan lingkaran 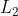 dengan jari-jari
dengan jari-jari  sehingga:
sehingga:
Jadi, jika 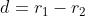 maka lingkaran pertama bersentuhan dengan bulat 2 di dalam
maka lingkaran pertama bersentuhan dengan bulat 2 di dalam
. Perhatikan gambar berikut!
Perhatikan gambar berikut!
 |
| Lingkaran pertama dengan bulat 2 sepusat |
Jadi, jika 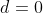 maka Lingkaran pertama dengan bulat 2 sepusat
maka Lingkaran pertama dengan bulat 2 sepusat
4. Lingkaran berpotongan dengan lingkaran
Perhatikan gambar berikut!
Gambar di atas, ditarik kesimpulan bahwa:
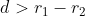 dan
dan 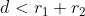
- AB merupakan tali busur sekutu
- Sentral
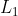
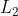 membagi dua tegak lurus tali busur AB
membagi dua tegak lurus tali busur AB - garis tersebut merupakan garis kuasa
Jadi, jika 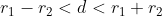 maka
maka Lingkaran pertama berpotongan dengan bulat 2
Ingat, dalam menyeleksi jarak antara sentra bulat yaitu  , maka penting dipahamai jarak dua titik
, maka penting dipahamai jarak dua titik \,&space;\,&space;dan\,&space;\,&space;(x_{2},y_{2})) yaitu:
yaitu:
Untuk mengetahui klarifikasi di atas amati pola soal berikut:
Contoh 1:
Diketahui sentra lingkaran  adalah (2, 6) dengan panjang jari-jari 2 cm. Sedangkan koordinat sentra lingkaran
adalah (2, 6) dengan panjang jari-jari 2 cm. Sedangkan koordinat sentra lingkaran  adalah (10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara lingkaran
adalah (10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara lingkaran  dan lingkaran
dan lingkaran  !
!
Pembahasan:
Dari soal sanggup dilihat apa saja yang dimengerti yaitu:
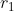 = 2 dan sentra L1 merupakan (2,6)
= 2 dan sentra L1 merupakan (2,6) = 6 dan sentra L2 merupakan (10,0)
= 6 dan sentra L2 merupakan (10,0)
sehingga dengan menggunakan rancangan jarak dua titik, maka sanggup diputuskan jarak kedua titik sentra Lingkaran yakni d:
^{2}+\left&space;(&space;y_{2}-y_{1}&space;\right&space;)^{^{2}}})
dan
Berdasarkan perkiraan di atas, diperoleh kesimpulan 10 > 8 atau 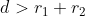 .
. Contoh 2:
Bagaimanakah kedudukan bulat x2 + y2 + 8x -4y – 5 = 0 dan bulat x2 + y2 + 4x – 2y – 11 = 0 ?
Pembahasan:
Dari persamaan L1 : x2 + y2 + 8x – 4y – 14 = 0 diperoleh sentra dan jari-jari bulat sebgai berikut: Pusat ( -4, 2) dan jari-jari = 5, dan dari persamaan L2 : x2 + y2 + 4x – 2y – 11 = 0 diperoleh sentra dan jari-jari yakni : Pusat (-2,1) dan jari-jari 4
sehingga dengan menggunakan rancangan jarak dua titik, maka sanggup diputuskan jarak kedua titik sentra Lingkaran yakni d:
^{2}+\left&space;(&space;y_{2}-y_{1}&space;\right&space;)^{^{2}}})
&space;\right&space;)^{2}+\left&space;(&space;1-2&space;\right&space;)^{2}})
Berdasarkan perkiraan di atas, diperoleh kesimpulan :  atau .
atau .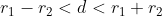
Jadi, jika 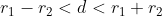 maka lingkaran pertama berpotongan dengan bulat 2
maka lingkaran pertama berpotongan dengan bulat 2
B. Tali Busur Sekutu
Tali busur bulat merupakan ruas garis dalam bulat yang menghubungkan 2 titik pada lingkaran. Untuk mengetahui tali busur sekutu, maka coba lihat gambar di bawah ini:
Dengan memperhatikan gambar di atas, maka garis AB merupakan tali busur sekutu dari bulat 1 dan bulat 2.
Jika diketahui:
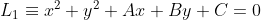
maka persamaan tali busur sekutu AB adalah:
Persamaan bulat yang lewat titik A dan B sanggup dinyatakan sebagai:
atau
=0) ,
, dimana m merupakan parameter
Untuk mengetahui bahan tali busur lihat pola soalnya di sini:
dengan jari-jari
dan lingkaran
dengan jari-jari
, dimana
>
. Misalkan d = jarak sentra lingkaran
dan
.
maka lingkaran
dan
tidak berpotongan, tapi di luar sesamanya.
=
+
, maka lingkaran
dan lingkaran
saling bersentuhan .







