Salam para BintangHalo semua pecinta pendidikan utamanya di bidang Matematika. Kali ini kita akan membahas bahan dasar dalam Dimensi Tiga yakni beberapa bangkit ruang yang menjadi dan sering timbul pada soal Ruang Dimensi Tiga. Nah,apa-apa saja yang sering timbul pada soal Dimensi Tiga tersebut? Kalian mesti mengetahui dan mengerti rumus-rumus dasar bangkit ruang tersebut.
Beberapa Bangun Ruang
1. Kubus
Kubus yakni bangkit ruang yang dibatasi oleh enam buah bidang persegi yang kongruen
Unsur-unsur pada kubus terdiri atas:
- Rusuk (12 buah)
- Bidang sisi (6 buah)
- Titik sudut (8 buah)
- Diagonal sisi (12 buah)
- Diagonal ruang (4 buah)
- Bidang diagonal ( 6 buah)
Jika panjang rusuk kubus yakni s cm, maka rumus-rumus yang berlaku pada kubus :
- Panjang diagonal sisi/bidang kubus adalah
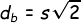
- Panjang diagonal ruang kubus adalah
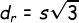
- Luas bidang diagonal kubus adalah
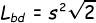
- Volume kubus adalah

- Luas Permukaan Kubus adalah
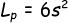
Contoh 1:
Diketahui kubus ABCD.EFGH dengan panjang rusuk 5 cm. Tentukanlah :
(a) Panjang diagonal bidang
(b) Panjang diagonal ruang
(c) Luas bidang diagonal
(d) Volume kubus
(e) Luas permukaan kubus
Penyelesaian:
Karena dikenali panjang rusuk 5 cm, maka:
(a) Panjang diagonal bidang = 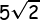 cm
cm (b) Panjang diagonal ruang = 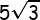 cm
cm (c) Luas bidang diagonal = 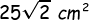
(d) Volume kubus = 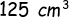
(e) Luas permukaan kubus = 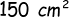
Contoh 2:
Diketahui kubus ABCD.EFGH dengan ukuran diagonal ruang 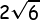 cm.Tentukanlah Luas Permukaan kubus dan volume kubus?
cm.Tentukanlah Luas Permukaan kubus dan volume kubus?
Penyelesaian:
Karena dikenali bahwa panjang diagonal ruang 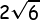 , maka :
, maka :
Diperoleh panjang rusuk kubus adalah 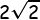 , maka:
, maka:
Volume kubus adalah:
dan Luas permukaan kubus adalah:
2. Balok
Balok yakni bangkit ruang yang dibatasi oleh enam buah bidang persegi panjang yang sepasang-sepasangnya kongruen
Unsur-unsur pada Balok terdiri atas:
- Rusuk (12 buah)
- Bidang sisi (6 buah)
- Titik sudut (8 buah)
- Diagonal sisi (12 buah)
- Diagonal ruang (4 buah)
- Bidang diagonal ( 6 buah)
Dalam balok ada panjang, lebar dan tinggi sehingga rumus-rumus penting yang berlaku adalah:
- Volume Balok adalah
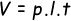
- Luas Permukaan Balok adalah
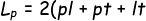)
- Panjang diagonal ruang adalah
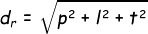
Contoh 3:
Diketahui balok ABCD.EFGH dengan ukuran rusuk AB = 5 cm, AD = 4 cm dan AE = 3 cm. Tentukanlah:
(a) Volume balok
(b) Luas permukaan balok
(c) Panjang diagonal bidang BG
(d) Panjang diagonal ruang
(e) Luas bidang diagonal BDHF
Penyelesaian:
Balok ABCD.EFGH dengan ukuran rusuk AB = 5 cm, AD = 4 cm dan AE = 3 cm
p = AB = 5 cm
l = AD = 4 cm
t = AE = 3 cm
a. Volume Balok
b. ) Luas permukaan balok
c. Panjang diagonal bidang BG
d. Panjang diagonal ruang
e. Luas bidang diagonal BDHF
3. Prisma
Prisma yakni sebuah bangkit ruang yang dibatasi oleh dua bidang sejajar dan kongruen dan beberapa bidang lain yang berpotongan menurut garis-garis yang sejajar. Memberi nama prisma diadaptasi dengan bentuk alas/atasnya. Prisma di bawah ini yakni prisma segitiga
Rumus-rumus pada prisma:
- Luas permukaan Prisma adalah
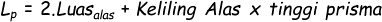
- Volume Prisma adalah
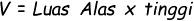
Contoh 4:
Suatu prisma terorganisir sisi empat dengan ukuran rusuk bantalan a cm dan rusuk tegak 5a cm. Jika luas permukaan prisma 88 cm maka tentukanlah volume prisma
Penyelesaian:
Perhatikan gambar berikut:
Sehingga volume prisma adalah:
4. Limas
Limas yakni sebuah bangkit ruang yang dibatasi oleh segitiga-segitiga yang berjumpa pada satu titik (atas) dan oleh bantalan sebuah sisi banyak. Memberi nama limas diadaptasi dengan bentuk alasnya.Limas disamping yakni limas segiempat.
Suatu limas dibilang limas teratur, kalau :
- Bidang alasnya berupa segi-n beraturan
- Proyeksi puncak pada bidang bantalan berimpit dengan sentra bulat luar bidang alasnya
Rumus-rumus penting pada limas:
- Luas permukaan = Luas bantalan + Luas segitiga dinding-dindingnya
- Volume Limas =
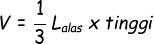
Contoh 4:
Diketahui limas T.ABCD dengan rusuk AB = 8 cm, AD = 6 cm dan AT = 9 cm. Tentukanlah :
(a) Tinggi limas
(b) Volume limas
(c) Luas bidang ABT
Penyelesaian:
Perhatikan gambar berikut !
a. Tinggi Limas
Untuk menyeleksi tinggi limas, pilih segitiga siku-siku APT yang siku -siku di P, maka:
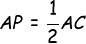
Sehingga AP = 5 cm, sehingga tinggi limas yakni TP sanggup diperoleh dari:
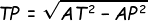
b. Volume Limas
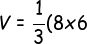(2\sqrt{14}))
c. Luas Bidang ABT
Perhaatikan segitiga ABT di bawah ini:
Dengan menyeleksi tinggi segitiga ABT yakni TQ apalagi dulu yang dipero;eh dari:

maka Luas ABT diperoleh yaitu
Baca Juga: 








