Materi , Referensi Dan Pembahasan Jarak Titik Dengan Titik, Jarak Titik Dengan Garis , Jarak Titik Dengan Bidang

Salam para Bintang

Halo semua pecinta pendidikan utamanya di bidang Matematika. Kali ini kita akan membahas bahan lanjutan yakni Jarak antara Titik dengan titik, jarak titik dengan Garis dan jarak titik dengan bidang. Nah, bagaimana cara memahaminya? Sebelumnya masuk ke bahan ini wajib kalian ketahui yaitu:

Jarak
Titik
Bidang

A. Jarak Titik dengan Titik

Jarak titik(objek) ke titik(objek) adalah adalah jarak terpendek yang ditarik dari kedua objek itu. Dalam geometri pun, jarak dua bangun didefinisikan selaku panjang ruas garis terpendek yang menghubungkan dua titik pada bangun-bangun tersebut.

Dalam menyeleksi jarak antara titik dengan titik hendaknya mengingat rancangan Teorema Phytagoras.

Perhatikan rujukan berikut, biar lebih paham :

Pada gambar diatas yang ialah suatu kubus ABCD.EFGH yang memiliki 8 buah titik yakni titk A, B, C, D , E,F, G dan titik H. Jadi, Jarak antara titik dengan titik pada kubus sungguh mudah kita pastikan apabila dikenali panjang rusuknya. Untuk memahaminya, amati rujukan soal berikut:

Contoh 1 :

Diketahui suatu kubus ABCD.EFGH dengan panjang rusuk kubus yakni 5 cm. tentukanlah jarak antara titik dengan titik berikut:

a. Titik A ke titik B

b. Titik A ke titik D

c. Titik A ke titik E

d. Titik C ke titik G

e. Titik D ke titik C

f. Titik B ke titik C

Jawab:

Perhatikan gambar berikut:

a. Jarak titik A ke titik B yakni 5 cm

b. Jarak titik A ke titik D yakni 5 cm

c. Jarak titik A ke titik E yakni 5 cm

d. Jarak titik C ke titik G yakni 5 cm

e. Jarak titik D ke titik C yakni 5 cm

f. Jarak titik B ke titik C yakni 5 cm

Contoh 2 :

Pada kubus ABCD.EFGH dengan rusuk 8 cm terdapat titik P di tengah - tengah AB. Tentukan jarak titik G ke titik P

Jawab:

Perhatikan gambar berikut:

Dengan mengitung dan memperhatikan apa yang diketahui,

Untuk menyeleksi PG , maka amati segitiga siku-siku PBC

$PB=\frac{1}{2}AB=\frac{1}{2}.8=4\, \, cm$

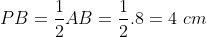
Kemudian menyeleksi panjang BG:

$BG=\sqrt{BC^{2}+CG^{2}}$

$BG=\sqrt{8^{2}+8^{2}}$

$BG=\sqrt{64+64}$

$BG=\sqrt{128}$

$BG=8\sqrt{2}$

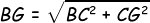
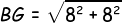
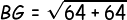
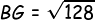
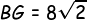
Kemudian kita pastikan panjang PG:

$PG=\sqrt{PB^{2}+BG^{2}}$

$PG=\sqrt{4^{2}+\left ( 8\sqrt{2} \right )^{2}}$

$PG=\sqrt{16+128}$

$PG=\sqrt{144}$

$PG=12\, cm$

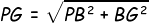
Jadi, jarak titik G ke titik P yakni 12 cm.

B. Jarak Titik dengan Garis

Jarak antara titik A dan ruas garis g yakni panjang ruas garis 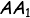$AA_{1}$ , dimana 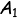$A_{1}$ merupakan proyeksi A pada garis g

Dalam menyeleksi jarak antara titik dengan titik hendaknya mengingat rancangan Teorema Phytagoras.

Perhatikan rujukan berikut, biar lebih paham :

Pada gambar diatas yang ialah suatu kubus ABCD.EFGH yang memiliki 8 buah titik yakni titk A, B, C, D , E,F, G dan titik H. Garis pada kubus ABCD.EFGH yakni AB, BC, CD,AD, AE,BF,CG,DH,EF,FG,GH,EH, AC, BD, EG, FH, AG,BH,DF,dan CE. Jadi, Jarak antara titik dengan titik pada kubus sungguh mudah kita pastikan apabila dikenali panjang rusuknya Untuk memahaminya, amati rujukan soal berikut:

Contoh 3 :

Diketahui suatu kubus ABCD.EFGH dengan panjang rusuk kubus yakni 5 cm. tentukanlah jarak antara titik dengan garis berikut:

a. Titik A ke garis CD

b. Titik B ke garis AD

c. Titik C ke garis FG

d. Titik C ke garis HG

e. Titik H ke garis FG

f. Titik F ke garis EH

Jawab:

Perhatikan gmbar berikut:

a. Jarak Titik A ke garis CD yakni 5 cm

b. Jarak Titik B ke garis AD adalah 5 cm

c. Jarak Titik C ke garis FG adalah 5 cm

d. Jarak Titik C ke garis HG adalah 5 cm

e. Jarak Titik H ke garis FG adalah 5 cm

f. Jarak Titik F ke garis EH adalah 5 cm

Contoh 2 :

Pada kubusABCD.EFGH dengan rusuk 6 cm, tentukanlah jarak titik B ke garis EG

Jawab:

Perhatikan gambar berikut:

Perhatikan segitiga BEG, dimana jarak B ke garis EG diwakili oleh ruas garis BP. Titik B tegak lurus dengan garis EG di titik P sehingga sanggup diwakili segitiga BEP. Kemudian kita akan pastikan panjang EP dan BE.

$BE=6\sqrt{2}$

$EP=\frac{1}{2}EG=\frac{1}{2}.6\sqrt{2}=3\sqrt{2}$

Maka panjang BP diperoleh dengan menggunakan rumus phytagoras diperoleh:

$BP=\sqrt{BE^{2}-EP^{2}}$

$BP=\sqrt{(6\sqrt{2})^{2}-(3\sqrt{2})^{2}}$

$BP=\sqrt{72-18}$

$BP=\sqrt{54}$

$BP=3\sqrt{6}\, cm$

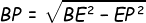
Jadi, jarak titik B ke garis EG adalah 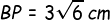$BP=3\sqrt{6}\, cm$

C. Jarak Titik dengan Bidang

Jarak antara titik A dan bidang V yakni panjang ruas garis 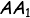$AA_{1}$ , dimana 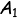$A_{1}$ merupakan proyeksi A pada bidang V

Dalam menyeleksi jarak antara titik dengan bidang hendaknya mengingat rancangan Teorema Phytagoras.

Perhatikan rujukan berikut, biar lebih paham :

Pada gambar diatas yang ialah suatu kubus ABCD.EFGH yang memiliki 8 buah titik yakni titk A, B, C, D , E,F, G dan titik H. Bidang pada kubus ABCD.EFGH yakni ABCD, ADHE, ABEF,BCFG,CDHG,EFGH. Jadi, Jarak antara titik dengan titik pada kubus sungguh mudah kita pastikan apabila dikenali panjang rusuknya Untuk memahaminya, amati rujukan soal berikut:

Contoh 5 :

Diketahui suatu kubus ABCD.EFGH dengan panjang rusuk kubus yakni 5 cm. tentukanlah jarak antara titik dengan garis berikut:

a. Titik A ke bidang EFGH

b. Titik B ke bidang CDHG

c. Titik C ke bidang ABEF

d. Titik C ke bidang ADHE

e. Titik H ke bidang ABCD

f. Titik F ke bidang ADHE

Jawab:

Perhatikan gmbar berikut:

a. Jarak Titik A ke bidang EFGH adalah 5 cm

b. Jarak Titik B ke bidang CDHG adalah 5 cm

c. Jarak Titik C ke bidang ABEF adalah 5 cm

d. Jarak Titik C ke bidang ADHE adalah 5 cm

e. Jarak Titik H ke bidang ABCD adalah 5 cm

f. Jarak Titik F ke bidang ADHE yakni 5 cm

Contoh 6 :

Pada kubus ABCD.EFGH dengan rusuk 6 cm terdapat titik P ditengahtengah AE. Tentukanlah jarak titik P ke BDHF

Jawab:

Perhatikan gambar berikut:

Dari gambar diperoleh bahwa:

Jarak P ke bidang BDHF sama dengan

$PR=\frac{1}{2}PQ$

$PR=\frac{1}{2}EG$

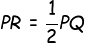
Karena 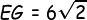$EG=6\sqrt{2}$ , maka:

$PR=\frac{1}{2}.6\sqrt{2}$

$PR=3\sqrt{2}$

Jadi, jarak titik P ke BDHF adalah 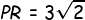$PR=3\sqrt{2}$

Baca Juga:

Buat lebih berguna, kongsi: